本文章是在阅读《集体智慧编程》过程中记录的一些对我有用的信息。

1. 相似度计算方式

1.1. 欧几里得距离

1.2. 皮尔逊相关系数

皮尔逊相关系数（Pearson Correlation）用于度量两个变量X和Y之间的相关（线性相关），其值介于-1到1之间。两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商： \[ \rho_{X,Y} = \frac{cov \left( X,Y \right)}{\sigma_X \sigma_Y} = \frac{E\left[\left( X - \mu x \right)\left( Y - \mu y \right) \right]}{\sigma_X \sigma_Y} \] 详细内容参见Wikipedia

1.3. Jaccard Coefficient

Jaccard Coefficient(又称Jaccard Index)用于测量样本集之间的相似度，它定义为：集合交集与集合并集的商，公式如下： \[ J\left( A, B \right) = \frac{\left|A \bigcap B \right|}{\left| A \bigcup B \right|} \] Jaccard Distance用于测量样本集之间的非相似度，它定义为：1 - Jaccard Coefficient，公式如下: \[ {J}_{\delta }\left( A, B \right) = 1-J\left( A, B \right) = \frac{\left|A \bigcup B \right| - \left|A \bigcap B \right|}{\left| A \bigcup B \right|} \] 详细内容参见Wikipedia

1.4. 曼哈顿距离

曼哈顿距离(Manhattan Distance)又称为出租车几何(Taxicab geometry)或方格线距离，它定义为：欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。 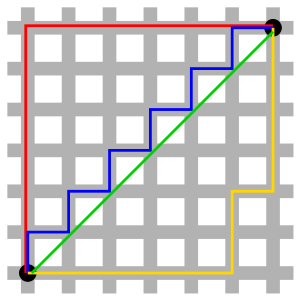上图中，红、蓝、黄线表示的曼哈顿距离都相等(12)，绿线表示欧几里得距离($6 * \sqrt{2} \approx 8.48$)。详情参见Wikipedia

更多的相似度计算公式可以参见Wikipedia