本文是LDA学习笔记系列文章的第5部分,主要介绍LDA在图像分类中的应用。
图像处理问题的第一步是特征提取,本文介绍的特征提取算法是SIFT(Scale-Invariant Feature Transform),该算法最早于1999年由David G. Lowe提出,2004年他在论文“Distinctive image features from scale-invariant keypoints”中对其加以发展和完善。通过SIFT算法可以将图像表示成一个特征的集合,然而这样的特征集合中的特征值都是不同的,为了能把图像表示成BOF(Bag of Feature),我们可以通过聚类算法将相近的特征表示为同一个特征,常用的聚类算法如:K-Means。至此,我们就可以统计每幅图片中各个特征出现的频率,获得特征的频率数据后就可以训练获得LDA模型。
SIFT算法分析
相关概念
- 关键点 就是在不同尺度空间的图像下检测出的具有方向信息的局部极值点。
- 尺度空间 通过对原始图像进行尺度变换,获得图像在多尺度下的尺度空间表示序列,对这些序列进行尺度空间主轮廓提取,并以该主轮廓为一种特征向量,实现边缘、角点检测和不同分辨率上的特征提取。尺度越大图像越模糊。实际上,在尺度空间理论中,是通过对图像进行模糊来模拟多尺度下的图像。直观上,图像的模糊程度逐渐增大,模拟了人在距离目标由近到远时目标在视网膜上的成像过程。
- 高斯卷积 图像的尺寸是自然存在的,而不是人为创造的。高斯核是唯一可以产生多尺度空间的线性核,一个图像的尺度空间L(x, y,σ) 定义为原始图像I(x, y)与一个可变尺度的2维高斯函数G(x, y,σ)的卷积运算。σ表示尺度。
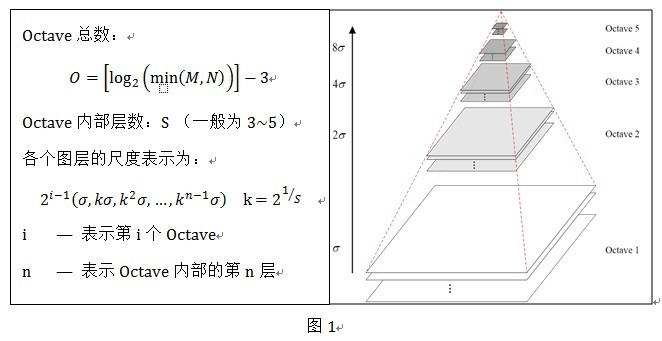
- 高斯金字塔 构建高斯金字塔分为两步:1)对图像做高斯平滑2)对图像做降采样(图像长宽各减半,总的大小变为原始图像的1/4)。一幅原始图像可以产生几组(Octave)图像,一组图像内部又包括几层(Interval)图像,为了让尺度体现连续性,相邻两层图像的尺度为K倍关系,同时相邻两组的同一层尺度为2倍关系,如下图1所示:
关键点检测
- LoG算子 Laplacian过滤器可以用于边缘检测,但是它对噪声数据非常敏感,所以一般先对图像进行一个平滑处理,常用高斯过滤器,这两步一起叫做LoG(Laplacian of Gaussian)算子
- DoG算子 通过推导可以看出,LoG算子与高斯核含函的差有直接关系,由此引入一种新的算子DoG(Difference of Gaussians),即高斯差分算子
- DoG金字塔 可以看出,LoG算子和DoG算子相差常数系数,而这并不会改变极值点的位置。因此我们在DoG算子中求得的极值点就是LoG算子的极值点,也正是我们需要的关键点。DoG在计算上只需相邻尺度的图像想减,因此简化了计算。对应DoG算子,我们要构建DoG金字塔,如图2左侧所示。
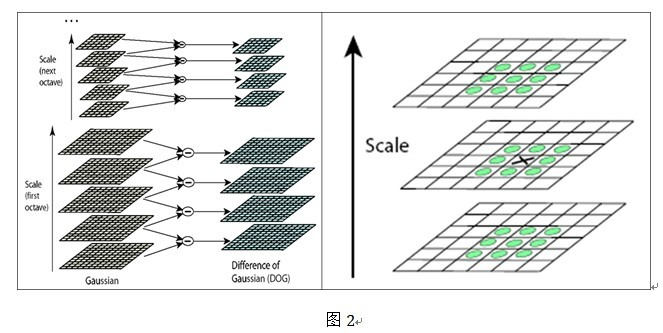
关键点是由DoG空间的局部极值点组成的,为了寻找DoG的极值点,每个像素点要和它所有的相邻点比较,相邻点包括了同尺度空间的8个相邻点,以及上下相邻尺度对应的2*9个点,共26个像素点,如图2右侧所示。在极值比较的过程中,每一组(Octave)图像的首末两层是无法进行极值比较的,为了满足尺度变化的连续性,我们在每一组图像的顶层继续用高斯模糊生成了3幅图像,因此高斯金字塔有每组S+3层图像,DOG金字塔每组有S+2层图像。
K-Means聚类
参考资料