本文是LDA学习笔记系列文章的第4部分，主要介绍一些比较常见的LDA的扩展模型

4. LDA扩展

4.1. Author-Topic模型

阅读论文: Michal Rosen-Zvi et al. “The Author-Topic Model for Authors and Documents” 2004
实验数据: NIPS data set

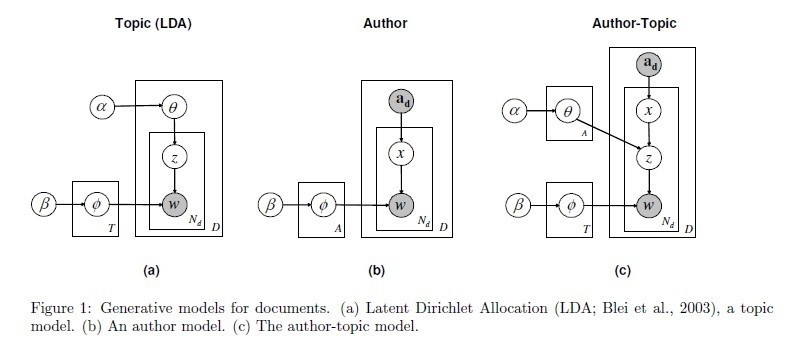
从上图可以看出，Author-topic模型是LDA模型与Author模型的结合。LDA模型的文本生成过程中，是根据doc-topic的分布$\theta$来选择下一个词的主题;而在Author-Topic模型，是根据doc-topic的分布$\theta$以及Author的主题分布两个因素结合来确定下一个词的主题分布。

4.2. 动态主题模型

阅读论文: David M. Blei et al. “Dynamic Topic Models” 2006
LDA模型假设文档的所包含的主题顺序是可交换的，但是实际上，文档的顺序会反映主题的演化过程，如：新闻文章、邮件等，因此本文提出了一种动态的主题模型。

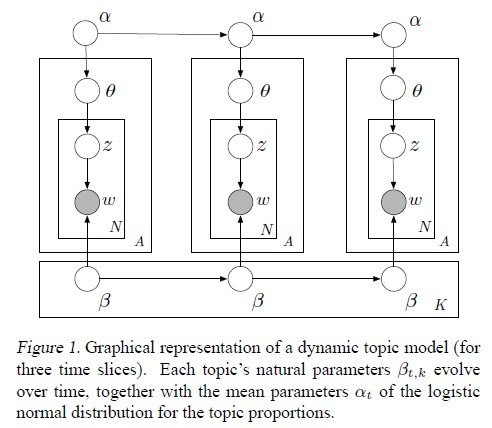
在动态主题模型中，文档集按时间顺序被分割成$t$个切片，每个切片内的子文档集都用主题模型建模。切片$t$内的topic-word分布$\beta_t$是由$t-1$切片内的topic-word分布$\beta_{t-1}$演化而来的，$\beta_{t,k}$表示切片$t$内主题$k$对应的topic-word分布。本文作者假定状态空间中的$\beta_{t,k}$是通过链式高斯分布(chaining Gaussian distributions)进化的，数学公式表达如下： \[ \beta_{t,k} \mid \beta_{t-1,k} \sim N \left( \beta_{t-1,k}, \sigma^2 I \right) \] 在LDA模型中，doc-topic分布$\theta$是通过Dirichlet分布求得的。在动态主题模型中，作者用$\alpha$均值的逻辑正态(logistic normal with mean $\alpha$)来表达$\theta$分布中的不确定性，切片之间$\alpha$的进化同样假定满足链式高斯分布，数学公式表达如下： \[ \alpha_t \mid \alpha_{t-1} \sim N \left( \alpha_{t-1}, \delta ^2 I \right) \] 出于模型的复杂性考虑，作者没有在动态主题模型中考虑主题之间的关联关系，但是作者在他的另一篇文章Correlated topic models中考虑了该问题。
参数评估时由于后验分布无法直接求解，所以论文中采用了Variational Kalman Filter和Variational Wavelet Regression这两种方法来做近似推理。